Highlighting: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 10: | Line 10: | ||
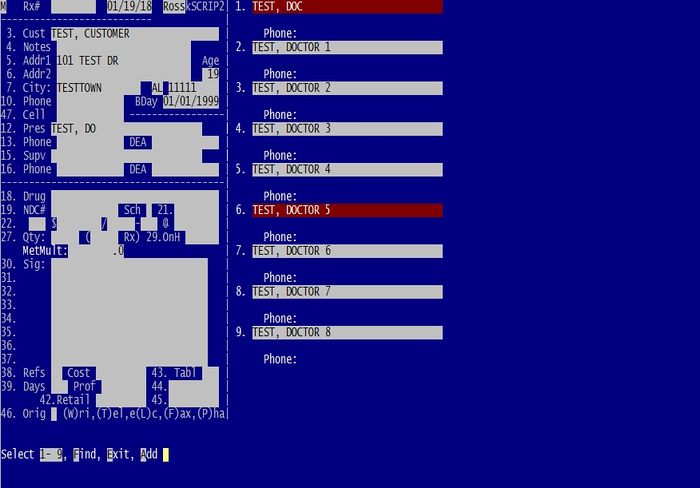
In the image below, note the two doctors with red highlighting in the pick list. | In the image below, note the two doctors with red highlighting in the pick list. | ||
[[File:HighDoc.jpg|700px|Note the two highlighted doctors in the pick list]] | [[File:HighDoc.jpg|700px|Note the two highlighted doctors in the pick list]] | ||
| Line 20: | Line 21: | ||
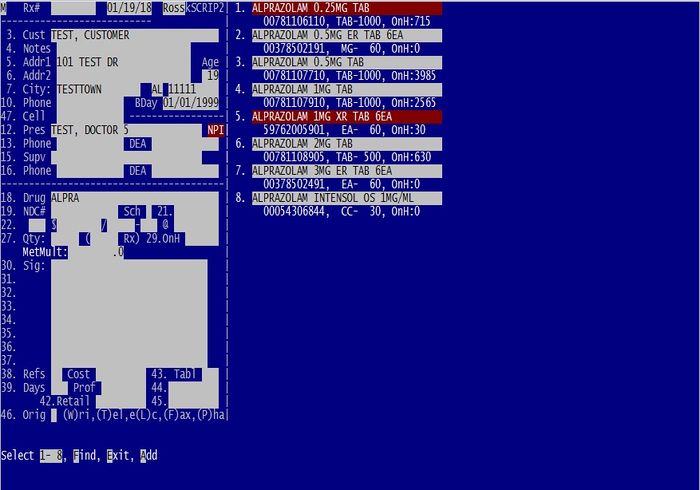
In the image below, note the two drugs with red highlighting in the list. | In the image below, note the two drugs with red highlighting in the list. | ||
[[File:HighDrg.jpg|700px|Note the two highlighted drugs in the pick list]] | [[File:HighDrg.jpg|700px|Note the two highlighted drugs in the pick list]] | ||
==Formulary Highlighting== | |||
In addition to highlighting individual drugs, you can highlight a group of drugs by linking each drug to a formulary code, and then setting your control file to highlight all drugs on that formulary code. | |||
'''To Set a Formulary Code on a Drug''' | |||
# Start in the '''Rx Processing Menu''' | |||
# Choose Option 11 '''Drug File Maint.''' | |||
# Search for the drug you wish to highlight. | |||
# On line 38 '''Code''' search for '''Formulary Code''' | |||
# Select a formulary code to attach to this drug. It can be any single letter or number. (Example '''3''' for 340B drugs, or '''C''' for compounds) | |||
Then set your system to highlight that formulary code: | |||
# Start in the '''Pharmacy Main Menu''' | |||
# Choose 3 '''Utilities''' | |||
# Choose 3 '''Business Control File''' | |||
# Select Option 6 '''Additional Rx Custom Screen 3''' | |||
# On line 3, set the Codes you want the QuickSCRIP system to highlight. | |||
Latest revision as of 16:27, 9 October 2018
QuickSCRIP offers the ability to highlight drugs and doctors in the pick-lists for RXFILL and EDIT, allowing you to call attention to particular doctors and drugs. The color of the highlight will vary based on the user's color scheme.
Doctor Highlighting
- Start in the Rx Processing Menu
- Choose Option 10 Doctor File Maint.
- Search for the doctor you wish to highlight.
- On line 22 Specialty mark the doctor with either /HL or /HILIT. Both commands function identically, one just saves character space.
In the image below, note the two doctors with red highlighting in the pick list.
Drug Highlighting
- Start in the Rx Processing Menu
- Choose Option 11 Drug File Maint.
- Search for the drug you wish to highlight.
- On line 38 Code search for Highlight this Drug in pick list
In the image below, note the two drugs with red highlighting in the list.
Formulary Highlighting
In addition to highlighting individual drugs, you can highlight a group of drugs by linking each drug to a formulary code, and then setting your control file to highlight all drugs on that formulary code.
To Set a Formulary Code on a Drug
- Start in the Rx Processing Menu
- Choose Option 11 Drug File Maint.
- Search for the drug you wish to highlight.
- On line 38 Code search for Formulary Code
- Select a formulary code to attach to this drug. It can be any single letter or number. (Example 3 for 340B drugs, or C for compounds)
Then set your system to highlight that formulary code:
- Start in the Pharmacy Main Menu
- Choose 3 Utilities
- Choose 3 Business Control File
- Select Option 6 Additional Rx Custom Screen 3
- On line 3, set the Codes you want the QuickSCRIP system to highlight.